The substitution effect of a price change under Hicksian approach and Slutsky approach has already been explained in the previous section. The compensated demand curve can be derived using these substitution effects in the same way in which demand curve and Engel demand curve were derived from price consumption curve (PCC) and income consumption curve (ICC) respectively. The derivation of compensated demand curve under the two approaches is illustrated in Fig. 5.50.
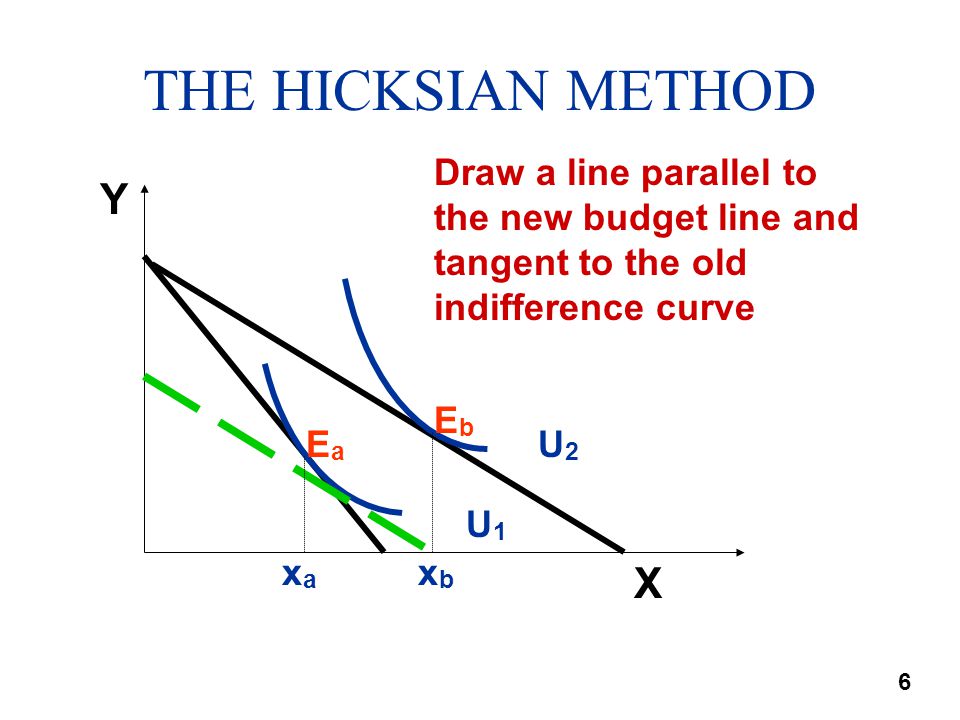
First, we consider the derivation of Hicksian compensated demand curve. In upper panel of Fig. 5.50 (a), the vertical axis shows the money income and the horizontal axis shows the quantity of commodity. The consumer is equilibrium at point ‘E’, where the initial budget line is tangent to indifference curve IC.
Now, suppose the price of commodity ‘X’ falls. The consumer’s equilibrium shifts to point ‘f on the new budget line and higher indifference curve IC1. Hicks-Allen substitution effect is shown as a movement along the same indifference curve IC.
ADVERTISEMENTS:
Under Hicksian approach, since the consumer is just compensated for the change in his real income on account of a price change, his level of satisfaction is restored to the original level through compensating variation. We know that the consumer substitutes relatively cheaper commodity.
In the figure, the consumer increases the quantity demanded for commodity ‘X’ from OX1 to OX2, while the quantity demanded of commodity ‘Y’ falls from OY1 to OY2. The Hicksian substitution effect in the figure measures the effect of change in relative prices, with real income constant, since two budget lines AB and CD (with different slopes) touch the same indifference curve IC at point ‘E’ and ‘G’. The movement from equilibrium point ‘E’ to equilibrium point ‘G’ reflects the substitution effect. It is equal to X1X2 in quantity terms.
In the lower panel diagram, the vertical axis shows the price of commodity ‘X’ and the horizontal axis shows the quantity of commodity ‘Y’. We observe that the quantities demanded corresponding to equilibrium points ‘E’ and ‘G’ are OX1 and OX3 respectively. When these quantities are plotted against their respective prices OA/OB and OA/OB” in the lower panel of the figure, we get Hicksian compensated demand curve CDH.
ADVERTISEMENTS:
Now, we consider the derivation of Slutsky compensated demand curve. In upper panel of Fig. 5.51(b), the consumer equilibrium shifts from point ‘E’ on the budget line AB to point ‘F’ on the budget line AB1 when price of the commodity X falls.
Again, money income of the consumer is shown along the vertical axis and the quantity demanded of commodity ‘X’ is shown along the horizontal axis. Indifference curves IC and IC1: touch the two budget lines at these points respectively. Now, the money income of the consumer is adjusted by taking away money, such that the consumer is able to purchase the original combination of the two commodities.
For this purpose, an imaginary budget line CD is drawn parallel to new budget line AB1, and passing through original equilibrium point ‘E’. We observe that the Slutsky approach over compensates the consumer and puts him at point, say’, G on a higher indifference IC2 on the budget line CD. The journey from point ‘E’ to point ‘G’ is the substitution effect, which is equal to X1X3 in quantity terms.
ADVERTISEMENTS:
In this lower panel diagram, the vertical axis shows the price of commodity ‘X’ and the horizontal axis shown the quantity demanded of commodity ‘X’. We observe that the quantities demanded corresponding to equilibrium points ‘E’ and ‘G’ are OX1 and OX3 respectively. When these quantities are plotted against their respective prices OA/OB and OA/OB1, in the lower panel of Fig. 5.50(b), we get Slutsky compensated demand curve CDS.
It is important to note that the compensated demand curve (or constant real income demand curve) under both the approaches is downward sloping. However, the Slutsky compensated demand curve is more elastic than the Hicksian compensated demand curve.
Further, Slutsky’s measure is more realistic as it relies on observable prices and quantities. This method does not require the exact shape of the indifference curve and puts the consumer on a higher indifference curve.
Since the sign of substitution effect is always negative, the compensated demand curve is always downward sloping, whether the commodity under consideration is a normal commodity, inferior commodity or a Giffen commodity. Thus, its shape is independent to the nature of the commodity.
The conventional demand curve for a normal commodity is even more elastic than Hicksian as well as Slutsky compensated demand curve, as it includes income effect besides substitution effect of a change in the price of a commodity.
For an inferior commodity, the elasticity of demand of the conventional demand curve will be less than that of the corresponding compensated demand curve. When income effect is equal to zero, the elasticity of demand of the conventional demand curve will be same as that of corresponding compensated demand curve.
For a Giffen commodity, unlike compensated demand curve, the conventional demand curve is upward sloping. The elasticity of demand for such demand curve depends upon the relative strength of the substitution effect on one hand and the income effect on the other hand. S. Slutsky’s measure is more realistic as it relies on observable prices and quantities. This method does not require the exact shape of the indifference curve and puts the consumer on a higher indifference curve.